Proximal Gradient Methods
- Proximal gradient methods are a powerful technique to solve non-convex inverse problems
- Problem: find the intersection of multiple (non-convex) sets (e.g. lines)
- Catch: Only allowed to "operate" on only one set a time
- Two Convex Sets
- Two Non-Convex Sets
- Multiple Non-Convex Sets
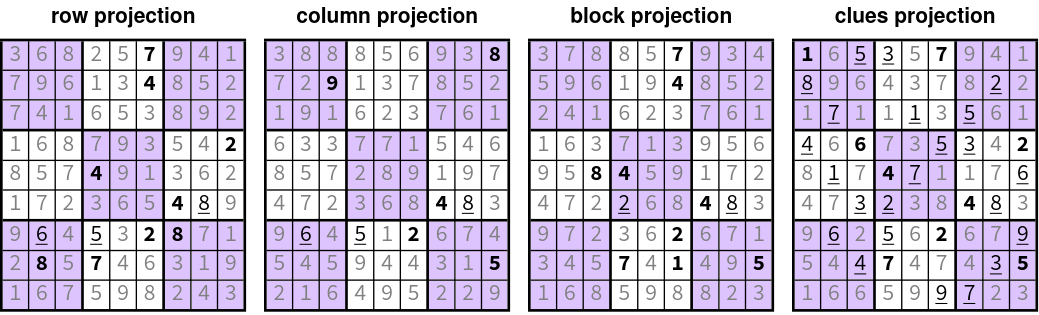
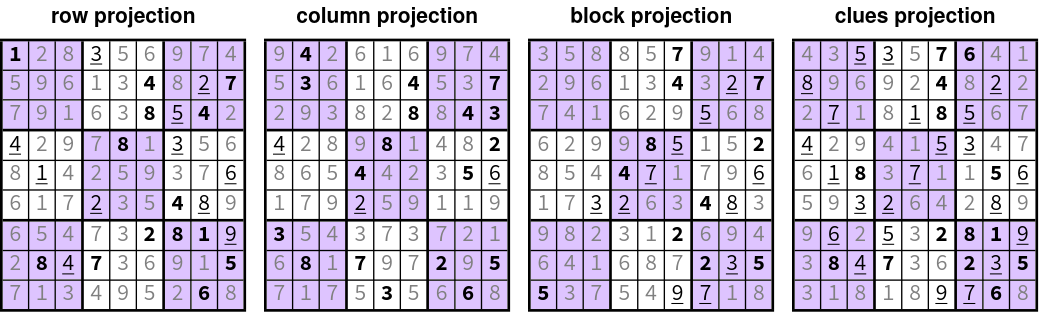
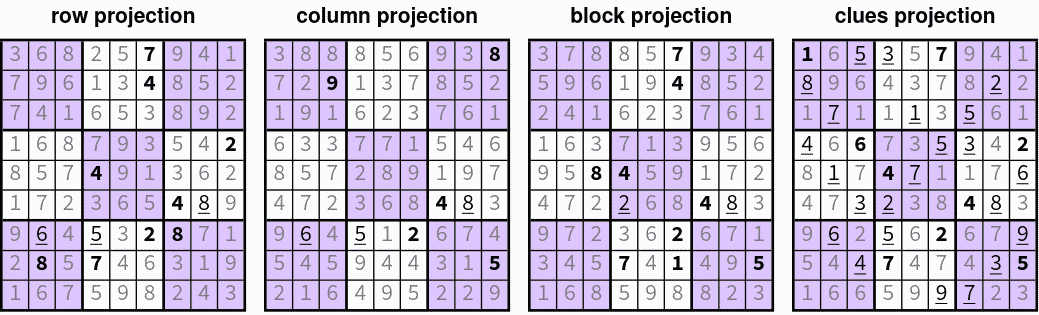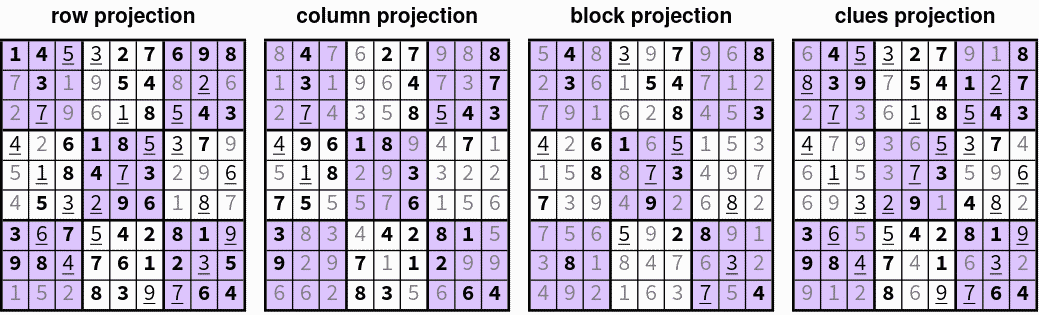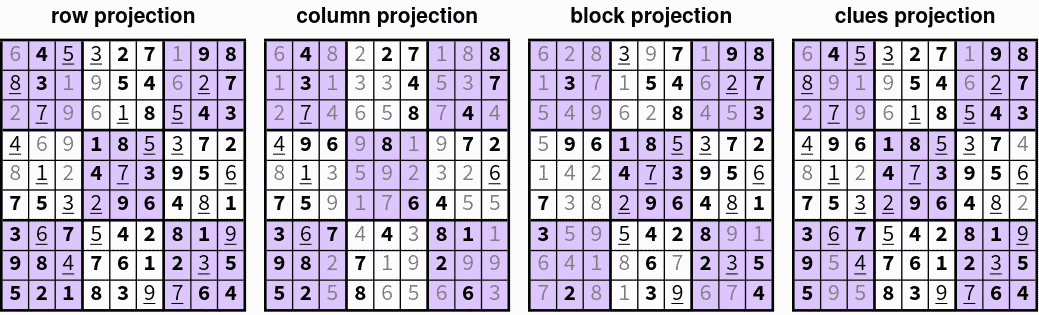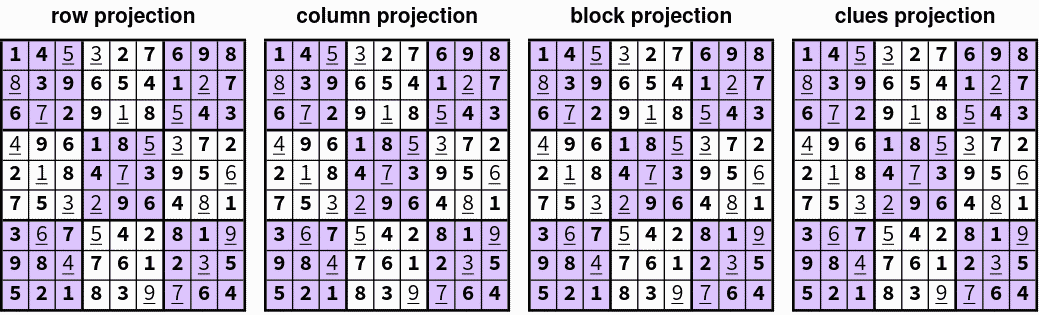
- Sudoku Puzzles
- Constraint satisfaction problem:
- Each row/column/3x3 block contains each of the numbers 1-9
- Solution must be consistent with a set of pre-defined clues
- Each constraint → projection to a non-convex set
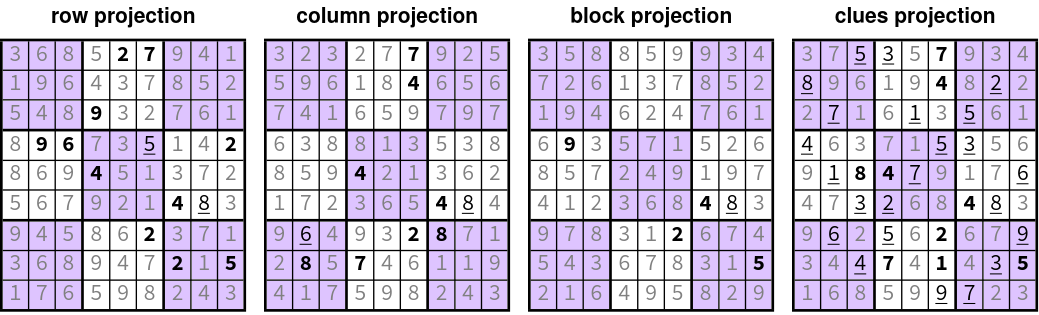
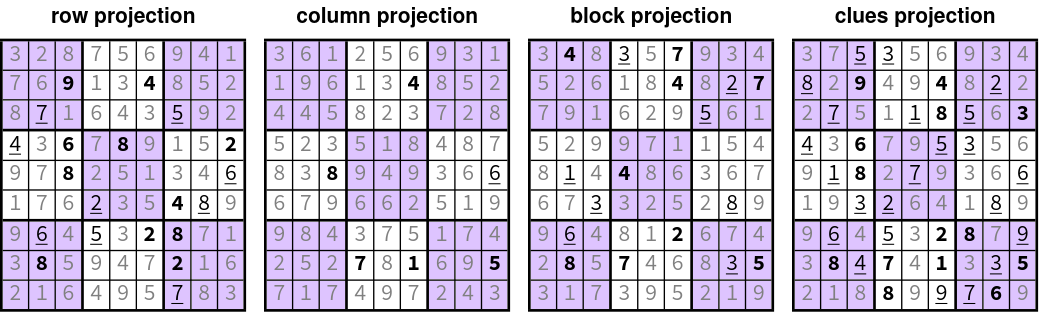
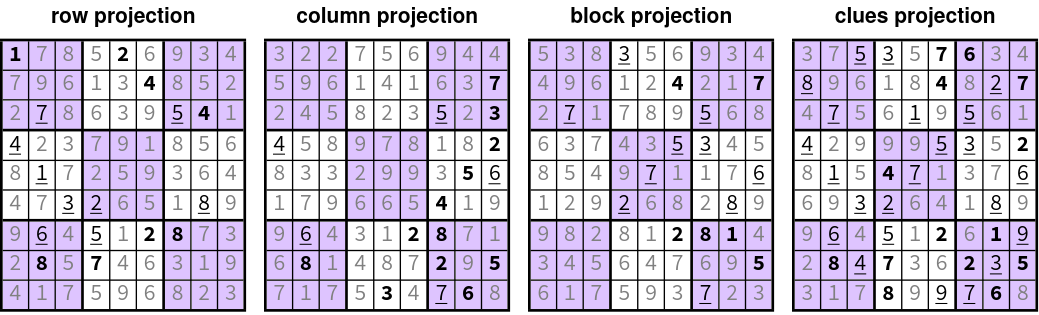
- This can be solved using iterative proximal gradient algorithms:
- Given a randomly-generated grid
- Apply each projection independently
- Average independent projections
- Rinse and repeat, until convergence
- iteration 01
- iteration 02
- iteration 03
- iteration 04
- iteration 05
- animated solution